I am happy to share the preprint of our paper A Closer Look At Invalid Action And Masking In Policy Gradient Algorithms, which can be found https://arxiv.org/abs/2006.14171. This is joint work by myself and my advisor Santiago Ontañón.
Invalid action masking is a technique employed most prominently in AlphaStar and OpenAI Five to avoid executing invalid actions in a given game state when the agents are being trained using policy gradient algorithms. In our paper, we find standard working mechanism of invalid action masking corresponds to valid policy gradient updates and, more interestingly, it works by applying a state-dependent differentiable function during the calculation of action probability distribution. Furthermore our investigation find invalid action masking to be empirically significant to the performance of policy gradient algorithms. Specifically, we show that invalid action masking scales well when the space of invalid actions is large, while the common approach of giving negative rewards for invalid actions will fail.
In this blog post, I will try to make our paper more accessible by using casual languages. In addition, I will also present many implementation details of invalid action masking.
Why are there invalid actions?
In more complicated games, the actions that the users can execute are usually dependent on the other game state that the users are in. For example, in the game of Dota 2, if the user is in the game state where he or she has zero gold, that the user could not issue the actions of buying any items. This means that different game states have different valid action spaces (i.e. different sizes of possible valid actions)
Recent advances in reinforcement learning utilize neural networks to represent the agent’s policy or value functions for the purpose of action selections. The use of neural networks usually indicates fix number of outputs, which makes it difficult to handle different valid action spaces. A common approach to simplify this problem is to construct a full action space that is the union of the sets of valid action spaces of all states.
What is the problem with full actions spaces?
Well, in simpler games, this really isn't much of an issue. The issues emerge when you have more complicated games such as StarCraft 2 or Dota 2. In Dota 2, as an example, the full action space is of 1,837,080 dimensions (https://cdn.openai.com/dota-2.pdf). Although it is not specified in the paper, I suspect the size of valid action spaces of any given states in Dota 2 should be only a fraction of 1,837,080. And here is the crux of the issue: when sampling an action from this full action space, it is much more likely to sample an invalid action than a valid action, resulting in significant amount of waste of time in sampling invalid actions that must be ignored by the game engine.
What are the solutions to handle invalid actions in full action spaces?
Very common approach to handle invalid actions is to give the agent negative rewards whenever an invalid action has been issued. The hope is to have the agent learn executing invalid actions is undesirable and therefore learn to not execute in invalid actions. At this point, however, it should be easy to see why this approach is kind of naïve and will fail in the actions space of 1,837,080 dimensions. The agent would have needed to spend a significant amount of time to learn the invalid actions in each state. Practically speaking, it is also possible that the agent will converge to a useless policy before learning any sequences of valid actions.
The approach used by AlphaStar and OpenAI Five is known as invalid action asking, which is the subject of our blog post and paper.
What is invalid action masking?
Invalid action masking is a technique utilized to mask out invalid actions in the full action space during the action selection process of policy gradient algorithms.
In the existing literature (https://arxiv.org/pdf/1708.04782.pdf, https://cdn.openai.com/dota-2.pdf), we find invalid action masking to be under documented. To the best of her knowledge, there is no literature providing detailed description of the working mechanism of invalid action masking. Generally speaking, existing work usually describe invalid action masking using only a few sentences. In addition, existing work also does not provide theoretical justification and generally provide no empirical investigation on the importance of invalid action masking.

This is why we will dive deep into the implementation of invalid action asking, hoping to provide insights by using an example.
A specific example
Consider an MDP with four actions a0, a1, a2, a3, and two states s0, s1, where the MDP reaches the terminal state s1 immediately after an action is taken in the initial state s0 and the reward is always +1. Further consider a policy pi to be parameterized by theta = [1.0,1.0,1.0,1.0] and the logits it produces is always theta. Normally, the action probability distribution is created by applying the softmax function on the unnormalized scores (logits). Suppose a0 is the action executed, and we have the following calculation:
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torch.distributions.categorical import Categorical
device = "cpu"
action = 0
advantage = torch.tensor(1.)
# no invalid action masking
print("=============regular=============")
target_logits = torch.tensor([1., 1., 1., 1.,] , requires_grad=True)
target_probs = Categorical(logits=target_logits)
print("probs: ", target_probs.probs)
log_prob = target_probs.log_prob(torch.tensor(action))
print("log_prob:", log_prob)
(log_prob*advantage).backward()
print("gradient:", target_logits.grad)=============regular=============
probs: tensor([0.2500, 0.2500, 0.2500, 0.2500], grad_fn=<SoftmaxBackward>)
log_prob: tensor(-1.3863, grad_fn=<SqueezeBackward1>)
gradient: tensor([ 0.7500, -0.2500, -0.2500, -0.2500])Now, we assume a2 is invalid. Invalid action masking helps to avoid sampling invalid actions by ``masking out'' the logits corresponding to the invalid actions. This is usually accomplished by replacing the logits of the actions to be masked by a large negative number M (e.g. M=-1e+8). Similarly, we assume a0 is the action being example, and we have the following calculation:
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torch.distributions.categorical import Categorical
device = "cpu"
action = 0
advantage = torch.tensor(1.)
# invalid action masking via logits
print("==================invalid action masking=============")
target_logits = torch.tensor([1., 1., 1., 1.,] , requires_grad=True)
# suppose action 1 is invalid
invalid_action_masks = torch.tensor([1., 1., 0., 1.,])
invalid_action_masks = invalid_action_masks.type(torch.BoolTensor)
adjusted_logits = torch.where(invalid_action_masks,
target_logits, torch.tensor(-1e+8))
adjusted_probs = Categorical(logits=adjusted_logits)
print("probs: ", adjusted_probs.probs)
adjusted_log_prob = adjusted_probs.log_prob(torch.tensor(action))
print("log_prob:", adjusted_log_prob)
(adjusted_log_prob*advantage).backward()
print("gradient:", target_logits.grad)==================invalid action masking=============
probs: tensor([0.3333, 0.3333, 0.0000, 0.3333], grad_fn=<SoftmaxBackward>)
log_prob: tensor(-1.0986, grad_fn=<SqueezeBackward1>)
gradient: tensor([ 0.6667, -0.3333, 0.0000, -0.3333])We now provide a list of our observations:
- When the invalid action masking is applied, there is virtually no chance of that the invalid action
a2will be sampled. - Invalid action masking actually changes the gradient calculation for the parameters of the policy. In particular, notice the gradient corresponding to the logits of the invalid action becomes zero.
Invalid Action Masking Produces a Valid Policy Gradient
The action selection process seems to be affected by this state dependent process that does not belong in the policy parameters. It is therefore natural to wonder if policy gradient still applies. That is, we wonder if the policy is still differentiable with respect to its parameters. As matter-of-fact, our analysis shows it is.
First, let us consider the process of invalid actually masking to be a function defined as below, where l(s) is the logits generated based on state s.
Then, we can calculate the re-normalized (masked) probability p'( . | s) as follows
One thing to notice is that inv_s either applies and identity function or a constant function, both of which are differentiable. Therefore inv_s is differentiable. This shows that the policy pi' is still differentiable with respect to it's parameters, suggesting the formulation of pi’ satisfies the assumptions of policy gradient theorem.
Invalid Action Masking as a State-Dependent Differentiable Function
Although in the previous section we showed that the working mechanism of invalid action masking is supported by policy gradient theorem, notice inv_s is a state-dependent differentiable function. That is, given two different states s, s’ with different sets of valid actions, and some fixed logits x, inv_s(x) != inv_s’(x).
To the best of my knowledge, the use of state-dependent differentiable function seems to be unseen in previous work, which generally has formulated the value function or the policy using state-independent differentiable functions such as sigmoid, tanh, exp, log, addition, multiplication, softmax. If you know any previous work that uses state-dependent differential functions to formulate the policy or the value function, please let me know and I would be happy to include it as related work.
Experimental setup
In the remaining parts of this blog post, we will examine the empirical importance of invalid action masking.
Evaluation environment
We use microrts (https://github.com/santiontanon/microrts) as our testbed, which is a minimalistic RTS game maintaining the core features that make RTS games challenging from an AI point of view: simultaneous and durative actions, large branching factors and real-time decision making. It is the perfect testbed for our experiments because the action space in microrts grows combinatorially and so does the number of invalid actions that could be generated by the DRL agent.
We now present the technical details of the environment for our experiments. In this blog post, I will try to keep the descriptions high-level; for lower level details, please refer to the paper.
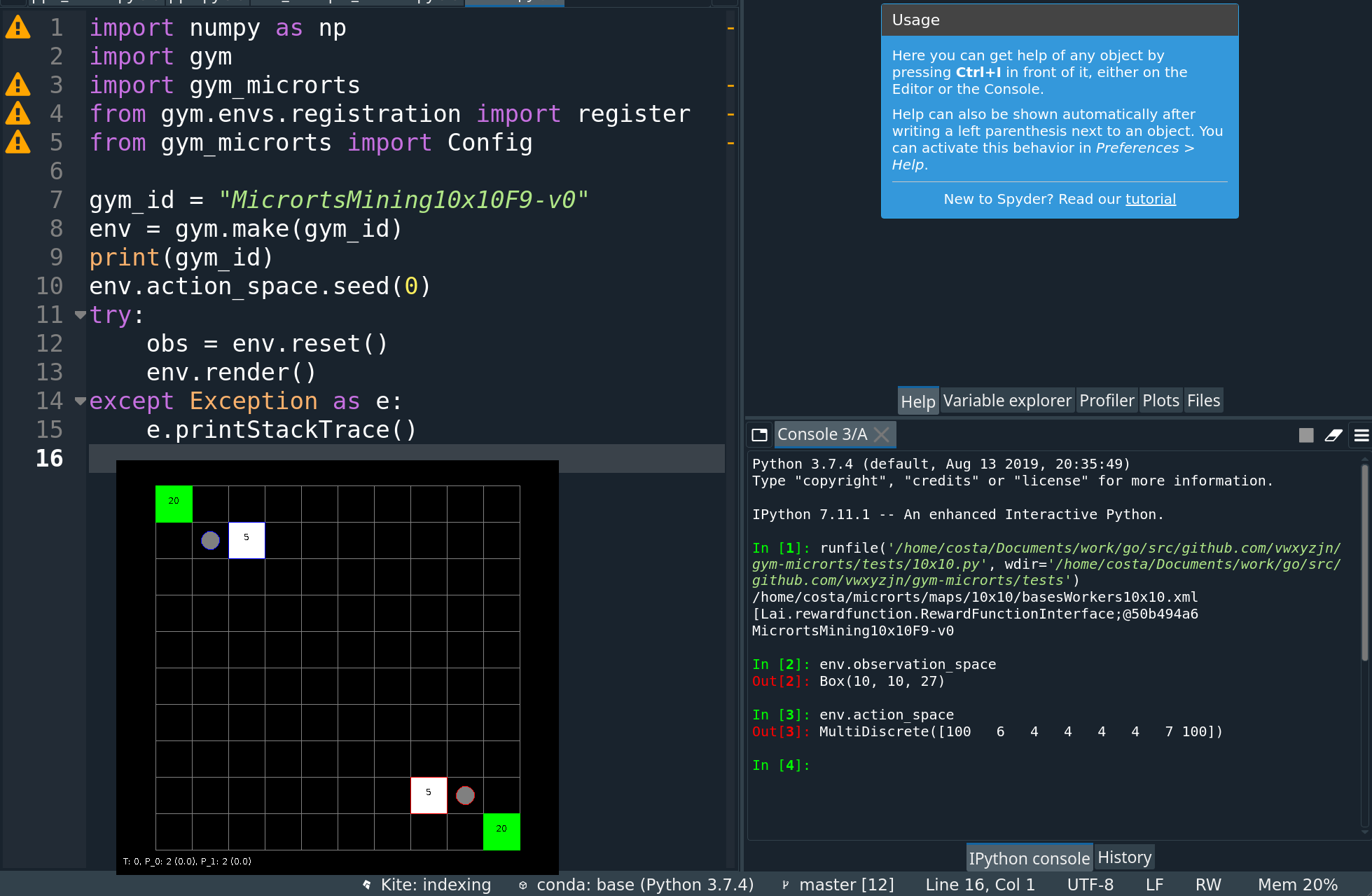
Observation space. As shown in the screenshot above, the observation space is of shape (h, w, n_f), where n_f is a number of feature planes that have binary values. The observation space used in this paper uses 27 feature planes, whose descriptions can be found in Table 1. A feature plane can be thought of as a concatenation of multiple one-hot encoded features. As an example, if there is a worker with hit points equal to 1, not carrying any resources, owner being Player 1, and currently not executing any actions, then the one-hot encoding features will look like the following:
[0,1,0,0,0], [1,0,0,0,0], [1,0,0], [0,0,0,0,1,0,0,0], [1,0,0,0,0,0]
The 27 values of each feature plane for the position in the map of such worker will thus be:
[0,1,0,0,0,1,0,0,0,0,1,0,0,0,0,0,0,1,0,0,0,1,0,0,0,0,0]
Action space. The action space it's a multi discrete with range of values being [h*w, 6, 4, 4, 4, 4, 7, h*w], where the meaning of the range can be found in Table 2. A sampled action vector might look like [ 5, 5, 2, 1, 0, 2, 2, 66], where the first component of the action vector represents the unit in the map to issue actions to, the second is the action type, and the rest of components represent the different parameters different action types can take. Depending on which action type is selected, the game engine will use the corresponding parameters to execute the action.
Rewards. We are evaluating our agents on the simple task of harvesting resources as fast as they can for Player 1 who controls units at the top left of the map. A +1 reward is given when a worker harvests a resource, and another +1 is received once the worker returns the resource to a base.
Termination Condition. We set the maximum game length to be of 200 time steps, but the game could be terminated earlier if the all of the resources in the map are harvested first.
Notice that the space of invalid actions becomes significantly larger in larger maps. This is because the range of the first and last discrete values in the action space, corresponding to Source Unit and Attack Target Unit selection, grows linearly with the size of the map. To illustrate, in our experiments, there are usually only two units that can be selected as the Source Unit (the base and the worker). Although it is possible to produce more units or buildings to be selected, the production behavior has no contribution to reward and therefore is generally not learned by the agent. Note the range of Source Unit is 4*4=16 and 24*24=576, in maps of size 4*4 and 24*24, respectively. Selecting a valid Source Unit at random has a probability of 2/16=0.125 in the 4*4 map and 2/576=0.0034 in the 24*24 map. With such action space, we can examine the scalability of invalid action masking.
Training algorithm
We use Proximal Policy Optimization to incorporate invalid action masking as the DRL algorithm to train our agents. It takes +22, -8 lines of code change to add invalid action masking to PPO in our implementation, as shown in https://www.diffchecker.com/yJG3niE6.
Strategies to Handle Invalid Actions
To examine the empirical importance of invalid action masking, we compare the following four strategies to handle invalid actions.
- Invalid action penalty. Every time the agent issues an invalid action, the game environment adds a non-positive reward
r_invalid ≤ 0to the reward produced by the current time step. This technique is standard in previous work (https://arxiv.org/abs/cs/9905014). We experiment withr_invalid \in {0, -0.01, -0.1, -1}, respectively, to study the effect of the different scales on the negative reward. - Invalid action masking. At each time step
t, the agent receives a mask on the Source Unit and Attack Target Unit features such that only valid units can be selected and targeted. Note that in our experiments, invalid actions still could be sampled because the agent could still select incorrect parameters for the current action type. We didn't provide a feature-complete invalid action mask for simplicity, as the mask on Source Unit and Attack Target Unit already significantly reduce the action space. - Naive invalid action masking. At each time step
t, the agent receives the same mask on the Source Unit and Attack Target Unit as described for invalid action masking. The action shall still be sampled according to the re-normalized probabilitypi'(.|s_t), which ensures no invalid actions could be sampled, but the gradient is updated according to probabilitypi(.|s_t). We call this implementation naive invalid action masking because its gradient does not replace the gradient of the logits corresponds to invalid actions with zero. - Masking removed. At each time step
t, the agent receives the same mask on the Source Unit and Attack Target Unit as described for invalid action masking, and trains in the same way as the agent trained under invalid action masking. However, we then evaluate the agent without providing the mask. In other words, in this scenario, we evaluate what happens if we train with a mask, but then perform without it.
Evaluation Metrics
We used the following metrics to measure the performance of the agents in our experiments:
r_{episode}is the average episode reward over last 10 episodes.a_nullis the average number of actions that select a {\em Source Unit} that is not valid over last 10 episodes.a_busyis the average number of actions that select a {\em Source Unit} that is already busy executing other actions over last 10 episodes.a_owneris the average number of actions that select a {\em Source Unit} that does not belong to Player 1 over last 10 episodes.t_solveis the percentage of total training time steps that it takes for the agents' moving average episode reward of the last 10 episodes to exceed 40.t_firstis the percentage of total training time step that it takes for the agent to receive the first positive reward.
Evaluation Results
We report the results in the following Table:
To make the results more readable, we also plot the average episode reward below
As always, some videos of the agents actually playing the game help. Below are some extracted videos of the trained agents in the 10x10 map.
Invalid action masking
Invalid action penalty w/ r_invalid=-0.01
Naive invalid action masking
Masking removed
Here is a list of observations.
Invalid action masking scales well. Invalid action masking is shown to scale well as the number of invalid actions increases; t_solve is roughly 12% and very similar across different map sizes. In addition, the t_first for invalid action masking is not only the lowest across all experiments (only taking about 0.05-0.08% of the total time steps), but also consistent against different map sizes. This would mean the agent was able to find the first reward very quickly regardless of the map sizes.
Invalid action penalty does not scale. Invalid action penalty is able to achieve good results in 4x4 maps, but it does not scale to larger maps. As the space of invalid action gets larger, sometimes it struggles to even find the very first reward. E.g. in the 10x10 map, agents trained with invalid action penalty with r_invalid=-0.01 spent a 3.43% of the entire training time just discovering the first reward, while agents trained with invalid action masking take roughly 0.06\% of the time in all maps. In addition, the hyper-parameter r_invalid can be difficult to tune. Although having a negative r_invalid did encourage the agents not to execute any invalid actions (e.g. a_null, a_busy, a_owner are usually very close to zero for these agents), setting r_invalid=-1 seems to have an adverse effect of discouraging exploration by the agent, therefore achieving consistently the worst performance across maps.
Masking removed still behaves to some extent. As shown in Figures~\ref{fig:sub:ar1}~\ref{fig:sub:ar2}, masking removed is still able to perform well to a certain degree. As the map size gets larger, its performance degrades and starts to execute more invalid actions by, most prominently, selecting an invalid {\em Source Unit}. Nevertheless, its performance is significantly better than that of the agents trained with invalid action penalty even though they are evaluated without the use of invalid action masking. This shows that the agents trained with invalid action masking can, to some extent, still produce useful behavior when the invalid action masking can no longer be provided.
KL Explosion of naive invalid action masking. According to Table above, the r_episode of naive invalid action masking is the best across almost all maps. In the 4x4 map, the agent trained with naive invalid action masking even learns to travel to the other side of the map to harvest additional resources. However, naive invalid action masking has two main issues: 1) As shown in Figures above, the average Kullback–Leibler (KL) divergence between the target and current policy of PPO for naive invalid action masking is significantly higher than that of any other experiments. Since the policy changes so drastically between policy updates, the performance of naive invalid action masking might suffer when dealing with more challenging tasks. 2) As shown in Table above, the t_solve of naive invalid action masking is more volatile and sensitive to the map sizes. In the 24x24 map, for example, the agents trained with naive invalid action masking take 49.14% of the entire training time to converge. In comparison, agents trained with invalid action masking exhibit a consistent t_solve=12% in all maps.
Concluding remarks
The primary goal of this paper is to carefully examine the implementation details of state-of-the-art Deep Reinforcement Learning methods. These methods usually feature a complicated machinery with a large number moving parts. It is imperative that we fully understand these moving parts that could be employed in creating intelligent decision systems in domains such as advertising, healthcare, robotics, and others.
In particular, our research points out the process of filtering out invalid actions, which has already been implemented in state-of-the-art methods, is empirically significant yet understudied by existing literature. Going forward, we hope to conduct more research to help properly attribute the success of DRL algorithms.
I hope this work is helpful to you. If you have any questions, feel free to comment down below.
A Note on Reproducibility
The source code of our experiments can be found https://github.com/vwxyzjn/invalid-action-masking. In addition, the metrics of the experiments are stored in https://wandb.ai/costa-huang/invalid-action-masking
For historical reasons, the experiments are done with an older implementation of PPO that does not include all the implementation details mentioned in The 32 Implementation Details of Proximal Policy Optimization (PPO) Algorithm. For example, it did not use the parallelized environment to speed up execution like it was done in the openai/baselines library.
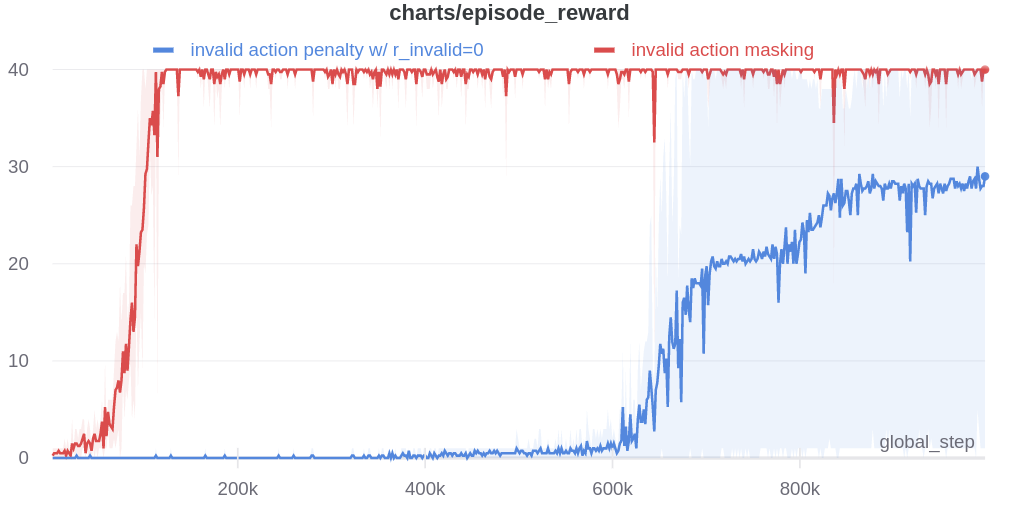
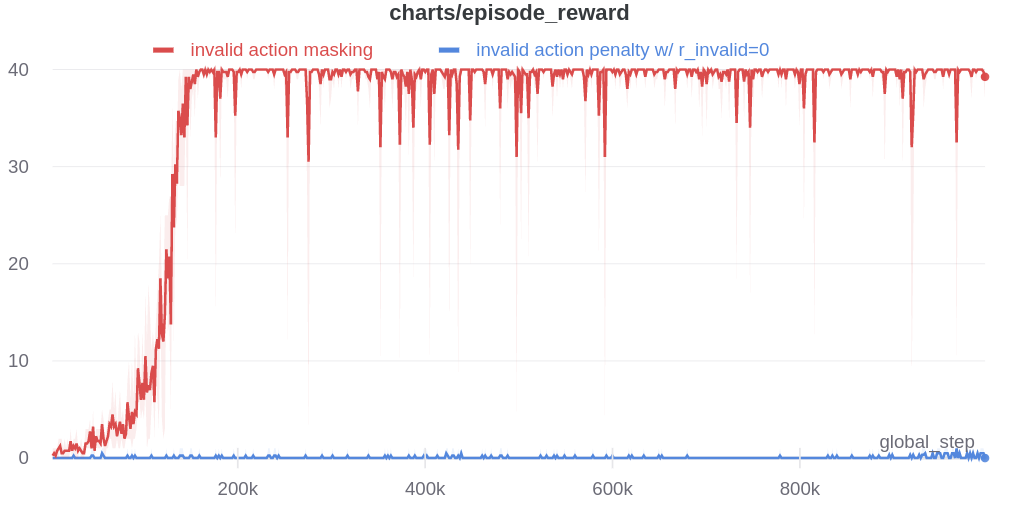
To ensure these details do not impact our results, I also re-run invalid action penalty with r_invalid=0 compared with invalid action masking using the new ppo implementation. And we show the results of our experiments below (https://app.wandb.ai/costa-huang/gym-microrts-mask4/reports/New-PPO-Implementation--VmlldzoxNTQ1MjQ):
Although it is the case that the new PPO implementation brings a performance boost to the agents trained with invalid action penalty with r_invalid=0 in 10x10 map, the agents does not learn anything until after 600k times steps. Additionally, In 24x24 map, invalid action penalty does not scale at all.
This is not surprising because none of the 32 implementation details for either Atari or Mujoco directly addresses the sparsity of valid actions in the full action space. Due to this finding, we will recommend interested researchers to use our new PPO implementation (https://github.com/vwxyzjn/gym-microrts/blob/master/experiments/ppo.py) that features the following implementation details. See my blog post The 32 Implementation Details of Proximal Policy Optimization (PPO) Algorithm for descriptions of these details.
- Invalid Action Masking
- Support for multi-discrete action space
- Clipped surrogate objective
- Generalized Advantage Estimation (GAE)
- Normalization of Advantages
- Value Function Loss Clipping
- Overall Loss Includes Entropy Loss
- Adam Learning Rate Annealing
- Mini-batch Updates
- Global Gradient Clipping
- Orthogonal Initialization of Weights and Constant Initialization of biases
- The Use of Parallelized Environment
- The Epsilon Parameter of Adam Optimizer being
1e-5
How to Cite Us
@misc{huang2020closer,
title={A Closer Look at Invalid Action Masking in Policy Gradient Algorithms},
author={Shengyi Huang and Santiago Ontañón},
year={2020},
eprint={2006.14171},
archivePrefix={arXiv},
primaryClass={cs.LG}
}
.svg?width=276&table=block&id=b75aecda-5431-4a72-a728-e06807e3932d)
.svg?width=230&table=block&id=c2c074c5-a1a5-44a1-8917-1590e2bd433d)
.svg?width=491&table=block&id=4e865cfb-6248-4252-9c5c-d583ace3f644)
.svg?width=557&table=block&id=53c7722f-94b0-4876-9e3d-129664b4d53c)
.svg?width=672&table=block&id=78463633-e39a-4123-acb6-a5694e4fafaf)