Recently I have been reading quite a lot on off-policy policy gradient, importance sampling, etc. When I was reading about Trust Region Policy Optimization (TRPO), I couldn't help but notice that the TPRO's objective doesn't have the log probability normally present in policy gradient methods such as A2C, as shown below.
This is really puzzling for me because the log probability trick [1] seems very standard in policy gradient methods. So what's the connection? After a bunch of searches, this answer by mglss [2] at StackExchange seems to have answered my question. In a nutshell, the log probability is still present in the TRPO's objective. Let's get the gradient of TRPO:
So apparently the log probability trick still works! Let's verify with code
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torch.distributions.categorical import Categorical
action = 0
advantage = torch.tensor(1.)
target_logits = torch.tensor([1., 1., 1., 1.,] , requires_grad=True)
behavior_logits = torch.tensor([2.3, 1., 1., 1.,], requires_grad=True)
target_probs = Categorical(target_logits)
behavior_probs = Categorical(behavior_logits)
TRPO_loss = -(target_probs.probs /
behavior_probs.probs.detach())[action] * advantage
print(TRPO_loss)
TRPO_loss.backward()
print(target_logits.grad)
# tensor(-0.5761, grad_fn=<MulBackward0>)
# tensor([-0.4321, 0.1440, 0.1440, 0.1440])
target_logits = torch.tensor([1., 1., 1., 1.,] , requires_grad=True)
behavior_logits = torch.tensor([2.3, 1., 1., 1.,], requires_grad=True)
target_probs = Categorical(target_logits)
behavior_probs = Categorical(behavior_logits)
importance_sampling = (target_probs.probs / behavior_probs.probs).detach()
# the .detach() above is **very important**
TRPO_log_loss = -target_probs.log_prob(
torch.tensor(action)) * importance_sampling[action] * advantage
print(TRPO_log_loss)
TRPO_log_loss.backward()
print(target_logits.grad)
# tensor(0.7986, grad_fn=<MulBackward0>)
# tensor([-0.4321, 0.1440, 0.1440, 0.1440])As shown by the results, the gradients generated by those two losses are the same. I want to take this chance to stress that the .detach() in the calculation of TRPO_log_loss is very important. If we don't add it, then the gradient calculated would have become the following, which is incorrect.
And empirically, the gradient is also incorrect.
target_logits = torch.tensor([1., 1., 1., 1.,] , requires_grad=True)
behavior_logits = torch.tensor([2.3, 1., 1., 1.,], requires_grad=True)
target_probs = Categorical(target_logits)
behavior_probs = Categorical(behavior_logits)
importance_sampling = (target_probs.probs / behavior_probs.probs)
# without the .detach() above
TRPO_log_loss = -target_probs.log_prob(
torch.tensor(action)) * importance_sampling[action] * advantage
print(TRPO_log_loss)
TRPO_log_loss.backward()
print(target_logits.grad)
# tensor(0.7986, grad_fn=<MulBackward0>)
# tensor([ 0.1669, -0.0556, -0.0556, -0.0556])Given this insight, I proceed to modify my PPO implementation using this kind of loss and verify if two losses will result in an identical gradient and results. Long story short, using the clipped objective and the log loss will result in different a gradient, but I don't feel compelled to investigate because that's sort of beyond the point of this post ... 😅 Instead, we experiment PPO without the clipped objective, then the gradient and trained policy will be the same as shown below.
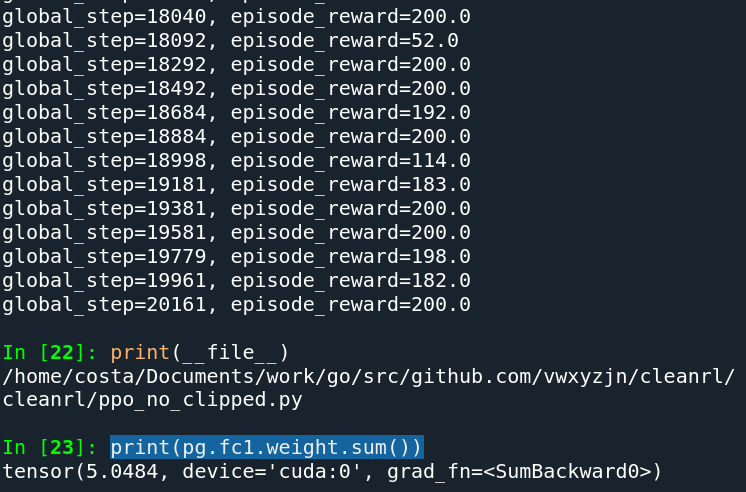
ppo_no_clipped.py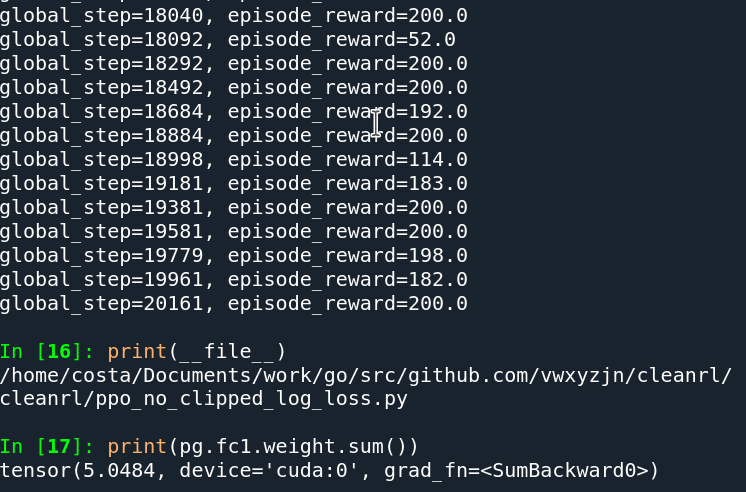
ppo_no_clipped_log_loss.pyThe only difference these two files them is the following
# in ppo_no_clipped.py
policy_loss = -torch.mean(importance_sampling *
torch.Tensor(advantages)[:step+1].to(device))
# in ppo_no_clipped_log_loss.py
policy_loss = -torch.mean(importance_sampling.detach() *
newlogproba * torch.Tensor(advantages)[:step+1].to(device))By this analysis, we see a nice connection between the objective of most policy gradient methods such as A2C and that of TRPO/PPO. Btw you can also run the code yourself at https://colab.research.google.com/drive/14A5GDrFiFzsBo6PF68yh4FW8EKMx5Zlt
Why major TRPO/PPO implementations do not use the log probability?
I suspect the reason is twofold. First, it makes it inconvenient to express the TRPO objective, which has then to be something like
Essentially, it has to be spelled out that the importance sampling does not contain any gradient for the target policy. Obviously, this is quite redundant.
Another reason might be purely in regards to implementation. As we demonstrated above, the person implementing the policy loss would need to consciously recognize the importance of detaching the gradient of the importance sampling from the gradient calculation of the policy. It is simply much easier to not having to worry about the detachment and leave it to the autograd package.
Conclusion
This article explores the reason that TRPO or PPO doesn't have the log probability as part of its objective. Both in theory and implementation, I show that the log probability is still there in the objective of TRPO or PPO. Hopefully this insight will be helpful to you :)

.svg?width=408&table=block&id=a46dd129-af60-489d-918f-882e2430285a)